| 1 |
| h19 |
| CS32 F18 |
| Name: | ||||
|---|---|---|---|---|
| (as it would appear on official course roster) | ||||
| Umail address: | @umail.ucsb.edu | |||
| Optional: name you wish to be called if different from name above. | ||||
| Optional: name of "homework buddy" (leaving this blank signifies "I worked alone" | ||||
h19: Heaps
| ready? | assigned | due | points |
|---|---|---|---|
| true | Tue 11/27 08:00AM | Tue 12/04 02:00PM |
You may collaborate on this homework with AT MOST one person, an optional "homework buddy".
MAY ONLY BE TURNED IN IN THE LECTURE LISTED ABOVE AS THE DUE DATE,
OR IF APPLICABLE, SUBMITTED ON GRADESCOPE. There is NO MAKEUP for missed assignments;
in place of that, we drop the four lowest scores (if you have zeros, those are the four lowest scores).
Reading: Heaps, DS 11.1 and 11.2, h19 Handout: http://cs.ucsb.edu/~richert/cs32/misc/h19-handout.pdf
- (10 pts) Fill in the information in the header. The following are required to get the 10 "participation" points.
- Filling in your name and umail address.
Also: For paper submission PLEASE submit on ONE SHEET OF PAPER, double-sided if at all possible. If you must submit on two printed sheets write name on BOTH sheets and no staples, paperclips, or folded corners.
- Filling in your name and umail address.
- According to DS, a "strict weak ordering" is a relation (i.e. a binary operator) that is irreflexive, antisymmetric, and transitive. An example given is
<. For each of the operators below, write True or False whether the operator has the three properties indicates, and then whether or not it meets the definition of a "strict weak ordering". The first two are done for you as examples.Operator Irreflexive Antisymmetric Transitive Strict Weak Ordering <True True True True <=False True True False (a) (4 pts) >(b) (4 pts) >= - The handout provides additional context for the textbook's description of heaps. In particular, the handout distinguishes between a max-heap and a min-heap. All the textbook's examples in 11.1 are max heaps. The handout also describes the "heap property" and the "heap shape" as being the two defining characteristics of a heap, with the "heap property" coming in two flavors: min-heap and max-heap.
For each of the binary trees below, indicate whether the tree has the min-heap property, the max-heap property, the heap shape, and then whether it is (or is not) as min-heap and/or a max-heap.
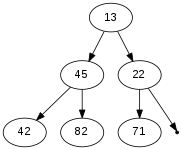
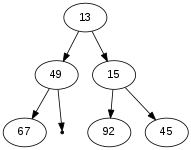
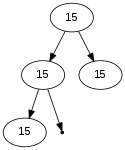
(3 pts) Circle one: min-heap-property: Y N min-heap-property: Y N min-heap-property: Y N (3 pts) Circle one: max-heap-property: Y N max-heap-property: Y N max-heap-property: Y N (3 pts) Circle one: heap-shape: Y N heap-shape: Y N heap-shape: Y N (3 pts) Circle one: is min-heap: Y N is min-heap: Y N is min-heap: Y N (3 pts) Circle one: is max-heap: Y N is max-heap: Y N is max-heap: Y N - One way to store a min-heap or max-heap is in an array. The rows of the array are stored in consecutive order: first row, then second row, then third row, etc. For reasons that will become apparent when you do the math, it is often the case that for reasons of "simplicity", we either ignore element [0] in the array (just treating it as wasted space), or we use it (somewhat inelegantly) to store the "occupancy" of the array. Thus, the n elements are stored in indices 1..n rather than 0..(n-1) as we would typically do in C, C++, Java, etc. This puts the root always in element [1].
Given this stipulation (1..n indexing), fill in the missing code in these three C++ functions that given the index of a node in this array, returns the index of the specified node. Note that for various reasons, the root is often "defined" as its own parent.
- (4 pts)
int parentOf(int index) { if (index <=0 ) return -1; if (index==1) return 1; // root is its own parent return ____________________________________; } - (4 pts)
int leftChildOf(int index) { if (index <= 0) return -1; return ____________________________________; } - (4 pts)
int rightChildOf(int index) { if (index <= 0) return -1; return ____________________________________; }
- (4 pts)
- DS describes two main operations on a max-heap data structure: adding an entry (Figure 11.1) which we will call insert and removing the maximum element (Figure 11.2) which we will call delete-max. For each of these operations, consider the book's implementation, then give runtime as either O(1), O(log n), O(n log n) or O(n2) along with a short justification of your answer:
- (5 pts) Insert:
- (5 pts) delete-max:
- (5 pts) Insert:
- (10 pts) Describe (in just a few sentences) how could you turn an unsorted (or sorted) array into a heap.